|
Was ist ein Polygramm?
... ... ... |
 ... ... |
Ein Polygramm ist ein regelmäßiger
Stern.
Es entsteht, indem man die Eckpunkte eines regelmäßigen
Vielecks so verbindet, dass man jeweils ein, zwei, drei ... Punkte überspringt. |
Erste
Sterne top
Brüche (p/q) mit q>1 kennzeichnen
die Sterne. Die erste Zahl gibt die Anzahl der Eckpunkte des umfassenden
Vielecks an, die zweite die "Sprungweite" beim Verbinden der Eckpunkte
(englisch density). Die Paare (p/q) heißen Schläfli-Symbole.
...
Polygramm
,,,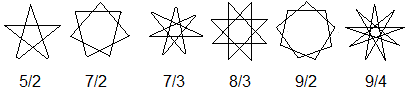 ,,, ,,, |
Man bezeichnet nur die Sterne als Polygramm (ohne
Zusatz), die beim Verbinden eine geschlossene Linie bilden. |
Zusammengesetztes
Polygramm
,,, ,,, ,,, |
Muss man beim Verbinden der Punkte mehrmals neu ansetzen,
erhält man ein zusammengesetztes Polygramm.
Die Sterne enthalten regelmäßige Vielecke,
die bei vielen Zacken auch Polygramme sein können.
Sie werden durch die gekürzten Brüche beschrieben. |
Da es nur einen regelmäßigen
Stern mit sechs Zacken gibt, bezeichnet man auch das zusammengesetze Hexagramm
als Hexagramm (ohne Zusatz).
Zu den ersten regelmäßigen
Sternen gibt es die Webseiten Pentagramm,
Hexagramm,
Heptagramm,
Oktagramm
und Nonagramm.
Verallgemeinerung
top
Unregelmäßiges Polygramm
... ... ... |
Wenn man vom Wort her kommt, müsste man auch den
nebenstehenden Stern als Polygramm bezeichnen, denn Polygramm heißt
"mit p Strichen". |
Stern
mit p Zacken
... ... ... |
Ein allgemeiner Stern entsteht, wenn man auf ein konvexes
n-Eck beliebige Dreiecke stellt.
Diesen Stern sollte man nicht mehr als Polygramm bezeichnen.
Er besteht nicht aus p, sondern aus 3p Strecken. |
Anzahl der Polygramme
top
Es stellt sich die Frage, welche Sterne (p/q) bei festem
p Polygramme sind, also welche Verbingungsstrecken im Vieleck geschlossen
sind. Darauf gehe ich auf meiner Webseite
30-Eck
ein.
...
...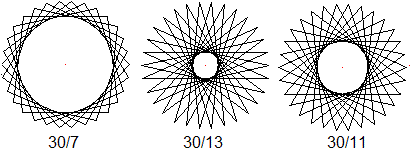 ... ... |
Danach sind nur drei Sterne Polygramme.
Wenn 30 und q teilerfremd sind, liegt ein Polygramm vor.
Die übrigen Figuren sind Vielecke oder zusammengesetzte
Polygramme. |
Verallgemeinerung
Wenn die beiden Kennzahlen in (p/q) teilerfremd sind,
so ist der zugehörige Stern ein Polygramm.
Überschlagene
Vielecke top
Gibt man ein regelmäßiges Fünfeck vor,
so gelangt man durch Verbinden der Eckpunkte durch eine geschlossenen Linie
nicht nur zum Fünfeck selbst und zum Pentagramm , sondern zu zwei
weiteren Figuren. Man bezeichnet sie als überschlagene Fünfecke.
Es gibt weiter 11 überschlagene Sechsecke und für
das Siebeneck mehr als 14.
...
Die Frage ist, wie viele überschlagene regelmäßige
Vielecke mit n Ecken es gibt.
Man kann versuchen, in der Sammlung von Folgen (oeis.org)
nach Fortsetzung der Folge 4, 13 zu suchen.
... |
Da sollte man die Zahlen des gleichseitigen Dreiecks
und des Quadrates,
nämlich 1 und 2, vorschalten. |
Man wird mit der Folge 1,
2 4, 13 in der Sammlung von Folgen oeis.org zwar fündig, doch
die Beschreibungen passen nicht.
Bei den angebotenen Folgen heißt die nächste
Zahl jeweils 57, 42, 50, 45 oder 31.
Winkel
an der Spitze top
...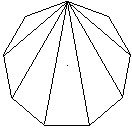 |
Verbindet man einen Eckpunkt mit allen anderen Eckpunkten
eines Vielecks, so entsteht die nebenstehende Figur.
Es gilt: Die Winkel zwischen den Diagonalen sind gleich. |
... |
Zum Beweis zeichnet man den Umkreis des Vielecks.
Alle Dreiecke im Vieleck haben gleich lange Sehnen als
Seite.
Nach einer Modifizierung des Umfangswinkelsatzes sind
alle Winkel zwischen den Diagonalen dann gleich. |
... ... ... |
Betrachtet man das symmetrische Dreieck und zeichnet
den Mittelpunkstswinkel ein, so lässt sich der Winkel berechnen.
Der Mittelpunktswinkel im p-Eck ist 360°/p.
Dann ist nach dem Mittelpunktssatz der Winkel an der
Spitze alpha = 180°/p. |
... ... ... |
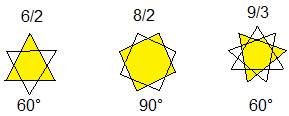
Für das Nonagramm z.B. gilt für die Winkel
an der Spitze der drei 9-Sterne
alpha(4) = 180°/9 = 20°,
alpha(3) = 3*180°/9 = 60°
und alpha(2) = 5*180°/9 = 100°. |
Allgemein gilt für den Stern p/q in umgekehrter Reihenfolge
alpha = [(p-2q)/p]*180°.
Winkel
der ersten Polygramme
...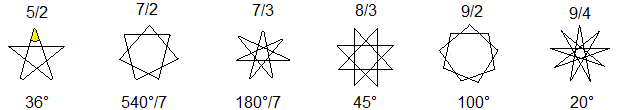 |
 |
Seitenlänge
eines Polygramms top
... ... ... |
Die Seite eines Polygramms ist eine Diagonale im zugehörigen
regelmäßigen Vieleck. |
... ... ... |
Auf meiner Webseite Regelmäßiges
Vieleck werden die Diagonalen, die eine Seite des regelmäßigen
Polygramms sein können, durch die Formel di = [a*sin(180°i/n)]/sin(180°/n)
erfasst.
Hier ist i = q und n = p. |
Es gilt also für die
Seitenlängen des Polygramms (p/q): s = a*sin(180°q/p)/sin(180°/p).
... |
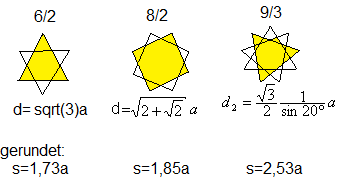 |
Die Terme stammen von meinen Webseiten regelmäßiges
Fünfeck,
Sechseck,
Siebeneck,
Achteck
und Neuneck.
Umkreis
und Inkreis top
...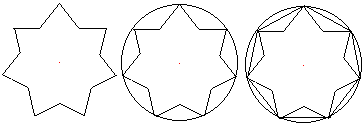 ... ... |
Der Umkreis eines Polygramms mit
dem Radius R ist der Kreis durch die Spitzen des Sterns oder der Umkreis
des umfassenden Vielecks.
Die Seitenlänge des umfassenden
Vielecks sei mit a gegeben. |
...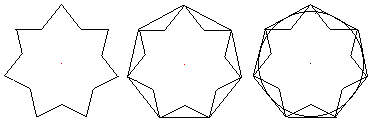 |
Der Inkreis eines Polygramms mit
dem Radius r ist der Inkreis des umfassenden Vielecks. |
...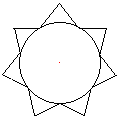 ... ... |
Man könnte meinen, der Kreis durch die inneren Spitzen
sei der Inkreis. Aber man verlangt von einem Inkreis einer Figur, dass
er Strecken von innen berührt. - Dieser Kreis ist der Umkreis des
inneren Vielecks. |
... ... ... |
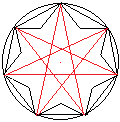
Zur Berechnung der Radien benutzt man das gelbe Dreieck.
Zunächst wird die Seitenlänge s bestimmt.
Im Dreieck ist sin(beta) = (s/2)/R und tan(beta) = (s/2)/r.
Dabei ist beta = (q/p)*180°.
Daraus folgt s=2R*sin[(q/p)*180°] und s=2r*tan[(q/p)*180°]. |
Andererseits wird im vorhergehenden Kapitel dieser Webseite
die Seitenlänge mit s = a*sin(180°q/p)/sin(180°/p) angegeben.
Eliminiert man die Seitenlänge s, so ist a = 2R*sin(180°/p)
und a = 2r*sin(180°/p).
Daraus ergeben sich die gesuchten Gleichungen R =
(1/2)a/sin(180°/p) und r = (1/2)a/tan(180°/p).
... ... ... |
Es fällt auf, dass in der Formel die "Spungweite"
q fehlt.
Aber wenn man mit einem Stern seinen Umkreis und sein
umfassendes Vieleck vorgibt und a festhält, so haben weitere Sterne
mit gleicher Zackenzahl den gleichen Umkreis. |
Flächeninhalt top
Vorweg: Für die Berechnung
des Flächeninhalts benötigt man zwei Formeln des regelmäßigen
Vielecks.
Der Flächeninhalt ist A(vieleck)
= (1/4)na²/tan(180°/n), der Innenwinkel ist alpha(vieleck) = [(n-2)/n]*180°.
Hier ist n=p.
... ... ... |
So soll vorgegangen werden:
Man gibt den Flächeninhalt des umfassenden Vielecks
vor und subtrahiert die Flächeninhalte der p gelben Dreiecke,
A = A1 - A2 |
... ... ... |
Der Flächeninhalt des umfassenden Vielecks ist A1
= (1/4)pa²/tan(180°/p). |
... ... ... |
Die Summe der Flächeninhalte der Dreiecke unter
den Seiten a berechnet man über das gelbe rechtwinklige Dreieck.
Es gilt A2 = p*(1/2)ah.
Man kommt weiter, wenn man den Winkel beta und die Höhe
h kennt. Beide sind durch die Zeichnung definiert.
|
Berechnung
des Winkels beta
Es gilt alpha+2beta = [(p-2)/p]*180° oder 2beta =
[(p-2)/p]*180°-alpha.
Der Winkel alpha ist der Winkel an der Spitze eines Sterns:
alpha = [(p-2q)/p]*180°.
Dann ist 2beta = (p-2)/p*180°-[(p-2q)/p]*180°=
[(2q-2)/p]*180° oder beta = [(q-1)/p]*180°.
Berechnung
der Höhe h
Im gelben Dreieck gilt tan(beta) = h/(a/2).
Dann ist h = (1/2)a*tan(beta) = (1/2)a*tan[(q-1)/p*180°].
Für die Gesamtfläche
der gelben Dreiecke gilt dann
A2 = p*(1/2)ah = p*(1/4)a²*tan[(q-1)/p*180°].
Der Flächeninhalt des
Polygramms ist
A = A1 - A2 = (1/4)pa²/tan(180°/p)-(1/4)pa²*tan[(q-1)/p*180°]
oder A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa².
Zackendreieck top
...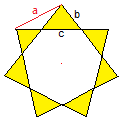 ... ... |
Ein Stern besteht aus einem regelmäßigen Vieleck,
auf dessen Seiten gleichschenklige Dreiecke stehen. Ihre Basis c und ihre
Schenkel b sollen berechnet werden. Der Stern sei wieder durch die Seite
a des umfassenden Vielecks gegeben. |
Bestimmung
von b
...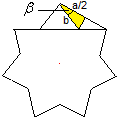 |
Zur Bestimmung der Seite b wird das gleiche Dreieck verwendet
wie bei der Flächenbestimmung.
Es gilt cos(beta) = (a/2)/b oder b = (a/2)/cos(beta).
Dabei ist beta = [(q-1)/p]*180°.
Dann ist b = (a/2)/{cos[(q-1)/p]*180°}. |
Bestimmung
von c
...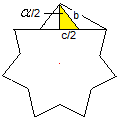 |
Im gelben Dreieck daneben gilt sin(alpha) = (c/2)/b oder
c = 2b*sin(alpha/2),
wobei alpha als Winkel an der Spitze [(p-2q)/p]*180°
ist.
Dann ist c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}.
Übrigens ist c auch die Seite des inneren Vielecks. |
Zusammenstellung
der Formeln top
An einem Heptagramm werden bekannte Größen
eines Polygramms angezeigt.
... |
alpha - Winkel an der Spitze
s - Seitenlänge
c - Grundseite einer Zacke
b - Schenkel einer Zacke |
R - Radius des Umkreises
r - Radius des Inkreises
A - Flächeninhalt des Sterns
a - Seitenlänge des umfassenden Fünfecks |
Wenn die Seite a des umfassenden
Vielecks (Polygons) gegeben ist, so gelten für den p/q-Stern die folgenden
Formeln.
Winkel an der Spitze alpha
Seitenlänge s
Grundseite einer Zacke c
Schenkel einer Zacke b
Radius des Umkreises R
Radius des Inkreises r
Flächeninhalt des Sterns A |
alpha = [(p-2q)/p]*180°
s = a*sin(180°q/p)/sin(180°/p)
c = a*{sin[(p-2q)/2p]*180°}/{cos[(q-1)/p]*180°}
b = (a/2)/{cos[(q-1)/p]*180°}
R = (a/2)/sin(180°/p)
r = (a/2)/tan(180°/p)
A = (1/4) {1/tan(180°/p)-tan[(q-1)/p*180°]}pa² |
Polygramme im
Internet top
Deutsch
Online-Rechner
Geometrierechner
Wikipedia
Stern
(Geometrie), Enneagramm
Englisch
Arthur Lee (Geogebra Animation)
star polygon
exploration
Dan Peters
Star
Polygon Generator
Eric W. Weisstein (World of Mathematics)
Star
Polygon
Hedrondude's Home Page (Jonathan Bowers)
Regular
Polygons and Other Two Dimensional Shapes
Wikipedia
Star
polygon, List
of regular polytopes#Stars
Französisch
Robert FERRÉOL (mathcurve)
POLYGONE
RÉGULIER et POLYGRAMME, LINKED
POLYGRAM, OCTOGONE
et OCTOGRAMME,
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
04/2024 Jürgen Köller
top |
 ...
... ...
...
 ,,,
,,, ,,,
,,, ...
... ...
...
 ...
...



 ...
... ...
...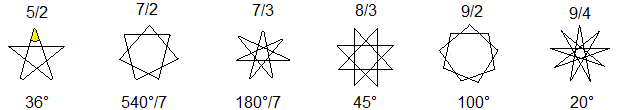

 ...
... ...
...
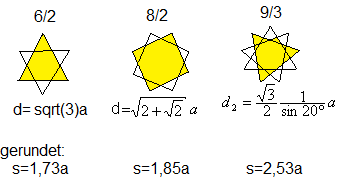
 ...
...
 ...
... ...
... ...
... ...
... ...
... ...
...

