|
Was ist ein abgestumpftes Tetraeder?
... ...
|
Ein abgestumpftes Tetraeder
ist ein Körper, der von 4 regelmäßigen Sechsecken und 4
gleichseitigen Dreiecken gebildet wird. |
Es entsteht aus einem Tetraeder,
indem man an den Ecken dreiseitige Pyramiden passend abschneidet.
... ... |
Dazu teilt man die Kanten in drei gleiche Teile.
An den Ecken des Tetraeders entstehen vier gleichseitige
Dreiecke.
Die vier Seitenflächen des Tetraeders reduzieren
sich auf vier Sechsecke. |
Neben den 4+4=8 Seitenflächen
hat der abgestumpfte
Tetraeder
18 Kanten und 12 Eckpunkte.
Die beiden folgenden, nebeneinander
liegenden Bilder ermöglichen eine dreidimensionale Ansicht des Körpers.
undurchsichtig:
durchsichtig:
Da beim Tetraederstumpf (2) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört er zu den 13
archimedischen
Körpern.
Beschreibung top
Gegenüberliegende Flächen
... ... |
Dreieck- und Sechseckfläche liegen parallel zueinander. |
Parallelprojektionen
Ein Sechseck liegt vorne.
|
Ein Dreieck liegt vorne.
|
Die Seite eines Dreiecks liegt vorne (?).
|
Die gemeinsame Seite
zweier Sechsecke liegt vorne.
|
Eine Ecke liegt vorne.
|
Zwei Sechsecke liegen
senkrecht zur Zeichenebene.
|
Netz und Schlegel-Diagramm
Diagonalen
36 Flächendiagonalen
... ... |
Die Diagonalen der Sechsecke sind die Flächendiagonalen.
Das führt zu insgesamt 4*9=36 Flächendiagonalen
des Tetraederstumpfes. |
12
Raumdiagonalen
... ... |
Von jedem der 12 Eckpunkte gehen zwei gleich lange Raumdiagonalen
aus.
Das führt zu insgesamt 12 Raumdiagonalen. |
Bilanz
Auf meiner Seite Dreieckszahlen
steht: "Verbindet man n Punkte mit allen möglichen geraden Linien,
so ergeben sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für das abgestumpfte Tetraeder bedeutet das, dass
es (1/2)11*12=66 Verbindungslinien gibt.
Das sind die 18 Kanten, 36 Flächendiagonalen und
12 Raumdiagonalen.
Größen top
Das abgestumpfte Tetraeder sei durch die Kantenlänge
a gegeben.
Daraus lassen sich weitere Größen wie Radius
R
der Umkugel, Radius rk der Kantenkugel,
Radius rk der Kantenkugel, Volumen V, Oberfläche
O,
der Abstand r3 eines Dreiecks vom Mittelpunkt und der
Abstand r6 eines Sechsecks vom Mittelpunkt berechnen.
Herleitungen
Oberfläche O
Die Oberfläche setzt sich
aus den Flächeninhalten der vier Sechsecke und der vier Dreiecke zusammen.
Ein gleichseitiges Dreieck hat
den Flächeninhalt
(1/4)sqrt(3)a². Ein Sechseck besteht
auch aus sechs kongruenten Dreiecken.
Also ist die Oberfläche
O
= 4A6+4A3 = 6*4A3+4A3 = 28A3
=
28*[(1/4)sqrt(3)a²] = 7*sqrt(3)a², wzbw.
Volumen V
Vorweg: Das Volumen eines Tetraeders
der Kantenlänge a' beträgt V3' = (1/12)sqr(2)*a'³.
Man erhält das Volumen des
abgestumpften Tetraeders V, indem man vom Volumen des Ausgangstetraeders
V3' das vier-fache Volumen einer abgeschnittenen Pyramide
(V3) subtrahiert.
... ... |
Die abgeschnittene Pyramide der Kantenlänge a hat
das Volumen V3 = (1/12)sqrt(2)a³.
Nach dem ersten Strahlensatz gilt a = a'/3 und H = H'/3
und somit V3' = (1/12)sqr(2)*(3a)³. |
Das bedeutet V = V3' - 4V3
=
(1/12)sqr(2)*(3a)³ - 4(1/12)sqrt(2)a³ = (23/12)sqrt(2)a³,
wzbw.
Radius
R der
Umkugel
Vorweg:
> Die Höhe im gleichseitigen
Dreieck ist h = (1/2)sqrt(3)a.
> Der Radius der Umkugel des Ausgangstetraeders
ist R' = (1/4)sqrt(6)a'.
> Die Höhe im abgeschnittenen
Tetraeder ist H = (1/3)sqrt(6)a.
... ...
|
M sei der Mittelpunkt des Tetraeders. In das Tetraeder
legt man ein rechtwinkliges Dreieck mit den Seiten R, dem Abstand des Mittelpunkts
von einer Seitenfläche R'-H und 2/3h. Nach dem Satz des Pythagoras
gilt R² = (R'-H)²+(2/3h)²
= [(1/4)sqrt(6)(3a)-(1/3)sqrt(6)a]²+[(2/3)(1/2)sqrt(3)a]²
= ... = (22/16)a² oder
R = (1/4)sqrt(22)a, wzbw. |
Radius
rk der Kantenkugel
Bei archimedischen Körpern liegen die Kantenmitten
auf einer Kugel, der Kantenkugel.
... ... |
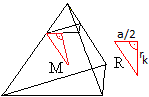Der Radius rk der Kantenkugel kann über
den Radius R der Umkugel bestimmt werden.
Im rechtwinkligen Dreieck gilt rk² =
R²-[(1/2)a]² = (22/16)a²-(1/4)a² = (18/16)a².
Dann ist rk= (3/4)sqrt(2)a, wzbw.. |
Abstand
r3
eines Dreiecks vom Mittelpunkt
Es gilt r3 = R'-H = (1/4)sqrt(6)a'-(1/3)sqrt(6)a
= (3/4)sqrt(6)a-(1/3)sqrt(6)a = (5/12)sqrt(6)a.
Abstand
r6
eines Sechsecks vom Mittelpunkt
Vorweg: Der Radius der Inkugel im Tetraeder der Kantenlänge
a' ist r = (1/12)sqrt(6)a'.
Dann ist r6 = (1/12)sqrt(6)(3a) = (1/4)sqrt(6)a.
Der Abstand zwischen Dreieck
und Sechseck ist (5/12)sqrt(6)a+(1/4)sqrt(6)a
= (2/3)sqrt(6)a.
Winkel
zwischen zwei Seitenflächen
Der Winkel zwischen zwei Sechsecken beträgt 70°32'.
Der Winkel zwischen Dreieck und Sechseck beträgt
109°28'.
Quelle (1)
Weitere Körpertop
Triakistetraeder
... ... |
Verbindet man die Mittelpunkte nebeneinander liegender
Mittelpunkte der Seitenflächen, so entsteht der duale Körper
des abgestumpften Tetraeders, das Triakistetraeder. |
... ... |
Das Triakistetraeder kann
als ein Tetraeder mit aufgesetzten, dreiseitigen Pyramiden angesehen werden. |
Vom
Tetraeder zum Oktaeder
... ... |
Aus einem Tetraeder kann ein zweiter Körper auch
durch Abschneiden dreiseitiger Pyramiden entstehen.
Dazu halbiert man die Kanten. Es entsteht ein Oktaeder. |
Basteleien top
Modell aus Stabmagneten
Aus 16 Kugeln und 24 Stabmagneten, die zwei Würfel
bilden, kann man einen Tetraederstumpf bauen.
Papiermodell
Abgestumpftes
Tetraeder im Internet top
Deutsch
Jürgen Meier
Abgestumpftes
Tetraeder
Wikipedia
Abgestumpftes
Tetraeder, Archimedischer
Körper, Catalanischer
Körper, Triakistetraeder
Englisch
Eric W. Weisstein (MathWorld)
Truncated
Tetrahedron, Archimedean
Solid, Small
Triakis Octahedron
Geneviève Tulloue ( Figures Animées pour
la Physique )
Polyhedra
(Applets)
G. Korthals Altes
Paper
Models of Truncated Tetrahedron
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Zeichnungen auf dieser Seite entstanden
mit Hilfe dieses Programmes.
Wikipedia
Truncated
tetrahedron, Archimedean
solid, Catalan
solid, Triakis
tetrahedron
Französisch
Robert FERRÉOL
TÉTRAÈDRE
TRONQUÉ
Referenzen top
(1) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961 (Seite 101)
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2007, überarbeitet 2013, Jürgen Köller
top |
