Was ist ein Kettenbruch?
Da die Schreibweise sperrig ist, kann man Klammern verwenden: 43/30 = 1+(1/(2+1/(3+1/4))). Durchgesetzt hat sich die übersichtliche Notation mit eckigen Klammern, 43/30 = [1; 2,3,4], die ich auch auf dieser Webseite verwende. Dabei stehen am Anfang die ganze Zahl 1 und nach einem Semikolon die weiteren ganzzahligen Anteile der gemischten Zahlen. Am Ende steht so der letzte Nenner 4. Mit dem Kettenbruch ist neben dem Dezimalbruch eine zweite Darstellung einer Zahl gegeben. Die Dezimalbruchdarstellung zeigt an, wo man die Zahl auf der Zahlengeraden findet. Der Kettenbruch gibt Näherungsbrüche von reellen Zahlen an, die vor allem für transzendente Zahlen von Interesse sind. Auf dieser Webseite habe ich das zusammengetragen, was ich interessant fand zum Thema Kettenbrüche.
Verallgemeinerungen top Man lässt sinnvollerweise für die auf dieser Seite verwendeten Variablen a0 ganze Zahlen und für die übrigen ak und bk reelle Zahlen außer Null zu. Im Allgemeinen begnügt man sich mit natürlichen Zahlen für ak und bk. Regelmäßiger Kettenbruch
Unendlicher regelmäßiger Kettenbruch
Allgemeiner Kettenbruch
Da verwendet man zum Beispiel die folgende Notation.
Auch der allgemeine Kettenbruch kann unendlich sein. Vom
Kettenbruch zum Bruch top
Als weitere Beispiele wähle ich einige gekürzte Brüche mit den Nenner 94.
Rekursionsformeln Es sei der Kettenbruch [a0; a1,a2,a3,...,ak] gegeben. Gesucht ist eine Formel für seinen Bruch Ak/Bk. Es gilt [a0; a1] = a0+1/a1
= (a0a1+1)/a1.
Es gilt [a0; a1,a2] =
a0+1/(a1+1/a2) = ... = [a2(a0a1+1)+a0]/(a1a2+1).
Es gilt [a0; a1,a2,a3]
= a0+1/[a1+1/(a2+1/a3)] = ...
= {a3[a2(a0a1+1)+a0]+a0a1+1}/[a3(a1a2+1)+a1]
Verallgemeinerung: Ak = akAk-1+Ak-2
und Bk=akBk-1+Bk-2
Anwendung Es soll für den Kettenbruch [1; 2,3,4,5,6,7] der Bruch x/y bestimmt werden.
Ergebnis: Der Kettenbruch [1; 2,3,4,5,6,7] führt
zum Bruch 9976/6961.
Die Rekursionsformel verwendet man für Computerprogramme, um von Kettenbrüchen zu Bruchzahlen zu gelangen. Näherungsbruch von 9976/6961 Die erste Zeile der folgenden Tabelle zeigt Kettenbrüche. Die zweite Zeile enthält die zugehörigen Brüche Ak/Bk, die dritte Zeile ihre Dezimalbruchdarstellungen. Die vierte Zeile gibt die Differenz zum gegebenen Bruch 6961/9972 an.
Mit Recht heißen die Brüche A1/B1 bis Ak-1/Bk-1 die Näherungsbrüche von Ak/Bk. Die Differenzen sind mit einer alternierenden Nullfolge vergleichbar. Diese Aussagen sind allgemein formuliert und gelten auch in dieser Allgemeinheit (1). Vom
Bruch zum Kettenbruch top
Multipliziert man beide Seiten der Gleichungen oben mit den Nennern, so erhält man > 73 = 2*29+15 > 29 = 1*15+14 > 15 = 1*14+1. Das ist das Vorgehen beim euklidischen Algorithmus zur Bestimmung des größten gemeinsames Teilers (ggT) zweier Zahlen. Man liest ggT(73,29) = 1 ab. Euklidischen Algorithmus Das Verfahren kann also auch dazu benutzt werden, zu der Bruchzahl 73/29 den Kettenbruch [2; 1,1,14] zu finden. > 73 = 2*29+15 > 29 = 1*15+14 > 15 = 1*14+1 Ein Vorteil dieser Bestimmung liegt auch darin, dass man die Rechnungen einem einfachen Computerprogramm überlassen kann. Das folgende Programm zur Bestimmung des größten gemeinsamen Teilers wird leicht abgeändert und ermittelt die Kettenbrüche von 73/29 und 9976/6961.
Unendliche Kettenbrüche
top
Oben steht [1; 2,2,2, ...] = sqrt(2). Herleitung Es gilt sqrt(2) = 1+sqrt(2)-1 =1+[(sqrt(2)-1)(sqrt(2)+1)]/[sqrt(2)+1] = 1+1/[1+sqrt(2)] Setzt man in der Gleichung sqrt(2) = 1+1/[1+sqrt(2)] rechts den Term 1+1/[1+sqrt(2)] ein, so erhält man 1+1/{2+1/[1+sqrt(2)]}. Setzt man das fort, so führt das zu einem unendlichen Kettenbruch 
Für die nächsten Quadratwurzeln gilt sqrt(4) = 2 sqrt(5) = [2; 4,4,4,4...]. Die Periode ist 4. sqrt(6) = [2; 2,4,2,4...]. Die Periode ist 2,4. sqrt(7) = [2; 1,1,1,4...]. Die Periode ist 1,1,1,4. sqrt(8) = [2; 1,4,1,4...]. Die Periode ist 1,4. sqrt(9) = 3 sqrt(10) = [3; 6,6,6,6...]. Die Periode ist 6. Ein bekannter Kettenbruch ist (1 + sqrt(5))/2 = [1; 1, 1, 1, 1, 1, 1, 1, 1, 1, ...]. Mehr auf meiner Seite Der Goldene Schnitt oder die stetige Teilung Transzendente Zahlen Für die fundamentalen transzendenten Zahlen Pi und e sind zahlreiche (schöne) Kettenbruchdarstellungen bekannt. Pi = 3+1²/(6+3²/(6+5²/(6+7²/(6+...)))) Man erkennt 3+1²/(6+3²/(6+5²/(6+7²/(6+...)))) und 3+1²/(6+3²/(6+5²/(6+7²/(6+...)))) 16/Pi = 5+1²/(10+3²/(10+5²/(10+7²/(10+...)))) Man erkennt: 5+1²/(10+3²/(10+5²/(10+7²/(10+...)))) und 5+1²/(10+3²/(10+5²/(10+7²/(10+...)))) 4/Pi = 1+1²/(3+2²/(5+3²/(7+4²/(9+...)))) Man erkennt zwei Folgen: 1+1²/(3+2²/(5+3²/(7+4²/(9+...)))) und 1+1²/(3+2²/(5+3²/(7+4²/(9+...)))) Pi/2 = 1-1/(3-2*3/(1-1*2/(3-4*5/(1-3*4/(3-6*7(/1-...)))))) Man erkennt 1-1/(3-2*3/(1-1*2/(3-4*5/(1-3*4/(3-6*7(/1-...)))))) und 1-1/(3-2*3/(1-1*2/(3-4*5/(1-3*4/(3-6*7(/1-...)))))) Quelle für die vier Darstellungen: (3), Seite 87 Oben erwähne ich den Bruch 6961/9976 = [1; 2,3,4,5,6,7]. Man gelangt von ihm zum unendlichen Kettenbruch [1; 2,3,4,5,6,7, ...]. Er wird auf der Seite von OEIS (URL unten) genannt. In der Spalte "Closed form" steht ein Fragezeichen. Eine Termdarstellung ist also nicht bekannt. Als Dezimalbruchdarstellung wird 1.433127426722311758317183455 genannt. Bei [1; 2,3,4,5,6,7, ...] denke ich an die normale Zahl 0,123456789101112..., die auch Champernowne-Konstante heißt. (Eine Zahl heißt normal, wenn unter den Dezimalen jede Ziffer gleich oft vorkommt. Das ist eine erste grobe Beschreibung.) Sie passt auf diese Webseite, da sie eine ungewöhnliche Kettenbruchdarstellung hat. (Mehr auf den Seiten von MathWorld) Für die eulersche Zahl e gibt es einen strukturierten, regelmäßigen Kettenbruch. e = [2; 1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...] Man erkennt [2; 1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...] und [2; 1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...] Quelle: OEIS, A003417 Näherungskonstruktion Das Siebeneck kann nicht exakt mit Zirkel und Lineal konstruiert werden. Es gibt eine Reihe von Näherungskonstruktionen.
Man kommt tan(alpha) beliebig nahe, wenn man den Kettenbruch tan(2pi/7) = [1; 3,1,15,31,1,3,...] wählt. Die ersten Näherungsbrüche sind 1, 4/3, 5/4, 79/63, 2454/1957, 2533/2020, 10053/8017, ... Kettenbruch im Internet top Deutsch Arndt Brünner
Bodo Werner
Günter Roolfs
Hans-Jürgen (matheplanet)
Nikolaus A. Bär
Wikipedia
Englisch Dr. Ron Knott
Eric W. Weisstein (MathWorld)
OEIS
Wikipedia
Referenzen top
URL meiner Homepage:
© April 2015 Jürgen Köller |
 ...
...


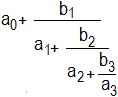


 ...
...


 ...
...